What is a database index
Index is a data structure to improve the speed of queries.
Every book has its table of contents. Similarly, an index is the “table of contents” for a database table. The database index is there to improve data query efficiency.
Why tree index
Before answering this question, let’s consider implementing an index with common data structures that supports fast look-ups like hashmap, array and binary search tree.
For hashmap, every insertion & deletion will just be constant time, query by key will also be constant time, but query by the key range from [KEY_i, KEY_j] will require a linear look-up time.
The array approach will have a amortized O(1) insertion time (append to tail). And both query by key and query by range will be O(1) if we map the table’s key into array index. However, the problem with array is that it doesn’t support dynamic insertion: insertion to the sorted keys will require linear time. Therefore, ordered array indexes are only suitable for static storage engines, i.e. storing data that will never be modified again.
Binary search tree will have O(logN) query complexity. To maintain O(logN) query complexity, one needs to keep the tree as a balanced binary tree. The update time complexity is also O(logN). Assuming the ratio of query operations over update operations is 1:1, then a binary search tree seems like the optimal choice among the 3. However, most database stores use n-ary trees instead of binary trees in practice. The reason is that the indexes is stored in the disk, and each disk seek operation is costly. Using a binary tree will lead to a much bigger height for a large number of nodes than an N-ary tree when N is significant, which gives rise to a higher number of seek operations considering the height difference.
B+ tree
B+ tree indexes are among the most common index data structures in database systems and are supported by almost all relational databases. Why? Because it is by far the most efficient data structure for sorting. Binary trees, hash indexes and red-black trees are far less efficient than B+ tree indexes in terms of disk-based storage of large amounts of data.
B+ tree indexes are characterized by a balanced tree based on disk, but the tree is very short, usually 3 to 4 levels, and can hold tens to hundreds of millions of sorted data. A short tree means less seeking, with only 3 or 4 I/Os to query data from tens or hundreds of millions of data. In addition, because the B+ tree is short, when doing the sorting, one only need to compare 3~4 times to locate the position where the data needs to be inserted, which is an excellent sorting efficiency.
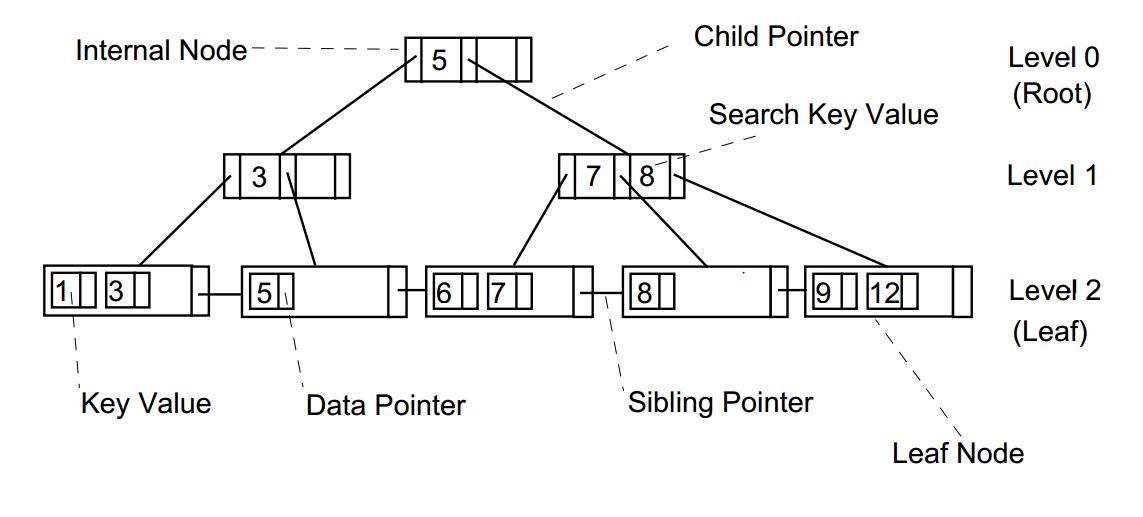
The B+ tree index consists of a root node, a non-leaf node, and a leaf node, where the leaf node holds all the sorted data.
All B+ trees start with a tree of height 1 and then slowly increase as data is inserted. Note that a B+ tree index of height 1 holds already sorted records, so if we want to do another query within a leaf node, we can quickly locate the data by only doing a binary search.
However, as more records are inserted into the B+ tree index, one page (16K) cannot hold so much data, so a splitting of the B+ tree occurs and the height of the B+ tree becomes 2. When the height of the B+ tree is greater than or equal to 2, the root and middle nodes hold index key pairs, consisting of (index key, pointer).
As we can see, in the B+ tree index above, if we want to look up a record with index key value 5, we first look up the root node and find the key-value pair (5, address), which means that records less or equal to 5 are in the next level of leaf nodes pointed to by the address. Then we can find the leftmost leaf node according to the address of the next level, and we can find the record with index key value 5 in the leaf node according to the binary lookup.
Efficiency
What is the theoretical maximum number of rows that a B+ tree index of height 2 can hold?
In MySQL InnoDB storage engine, a page size is 16K, and let’s say the key-value pair userId is of type LONG, then the root node can hold at most the following:
key-value pairs = 16K / key-value pair size (8+8) ≈ 1000
Assuming again that the size of each record in the table is 500 bytes, then:
The maximum number of records that can be stored in a leaf node is = 16K / size of each record ≈ 32
In summary, the maximum number of records that can be stored in a B+ tree index with a tree height of 2 is:
Total number of records = 1000 * 32 = 32,000
In other words, after sorting 35,200 records, the resulting B+ tree index has a height of 2. Searching for a record based on the index key in 32,000 records requires only 2 pages, a root and a leaf node, to locate the page where the record is located.
Similarly, the maximum number of records that can be stored in a B+ tree index with a tree height of 3 is:
Total number of records = 1000 (root node) * 1000 (intermediate nodes) * 32 = 32,000,000
We can conclude that:
- B+ tree indexes are typically 3 to 4 levels high, and a B+ tree of height 4 can hold about 5 billion records.
- Because of the low height of the B+ tree, queries are extremely efficient, and only 4 I/Os are needed to interpolate 5 billion records.
Implementation
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
namespace data {
struct Record {
//...
}
}
namespace index {
struct Address {
void* blockAddress;
std::size_t offset;
}
class Node
{
private:
Address *pointers; // A pointer to an array of struct {void *blockAddress, short int offset} containing other nodes in disk.
float *keys; // Pointer to an array of keys in this node.
int numKeys; // Current number of keys in this node.
bool isLeaf; // Whether this node is a leaf node.
friend class BPlusTree; // To access this class' private variables.
public:
Node(int maxKeys); // Takes in max keys in a node.
};
class BPlusTree
{
private:
MemoryPool *disk; // Pointer to a memory pool for data blocks.
MemoryPool *index; // Pointer to a memory pool in disk for index.
Node *root; // Pointer to the main memory root (if it's loaded).
void *rootAddress; // Pointer to root's address on disk.
int maxKeys; // Maximum keys in a node.
int levels; // Number of levels in this B+ Tree.
int numNodes; // Number of nodes in this B+ Tree.
std::size_t nodeSize; // Size of a node = Size of block.
// Updates the parent node to point at both child nodes, and adds a parent node if needed.
void insertInternal(float key, Node *cursorDiskAddress, Node *childDiskAddress);
// Helper function for deleting records.
void removeInternal(float key, Node *cursorDiskAddress, Node *childDiskAddress);
// Finds the direct parent of a node in the B+ Tree.
// Takes in root and a node to find parent for, returns parent's disk address.
Node *findParent(Node *root, Node *node, float lowerBoundKey);
public:
// Constructor, takes in block size to determine max keys/pointers in a node.
BPlusTree(std::size_t blockSize, MemoryPool *disk, MemoryPool *index);
// Search for keys corresponding to a range in the B+ Tree given a lower and upper bound. Returns a list of matching Records.
void search(float lowerBoundKey, float upperBoundKey);
// Inserts a record into the B+ Tree.
void insert(Address address, float key);
// Remove a range of records from the disk (and B+ Tree).
// Accepts a key to delete.
int remove(float key);
};
}