Common loop optimization techniques by compiler

Before optimizing a loop, we need to first define a loop in the control flow graph. Note that each node in a control flow graph is a basic block.

Identifying loops

Cycles in the control flow graph are not necessary loops. A loop is a subset S of nodes where:

S is strongly connected. In other words, for any two nodes in S, there is a path from one to the other using only nodes in S
There is a distinguished header node h∈S such that there is no edge from a node outside S to S\{h}

Dominators

Node d dominates node n in a graph (d dom n) if every path from the start node to n goes through d

Dominators can be organized as a tree

a -> b in the dominator tree iff a immediately dominates b

Back edge

Back edge is an edge from n to dominator d.

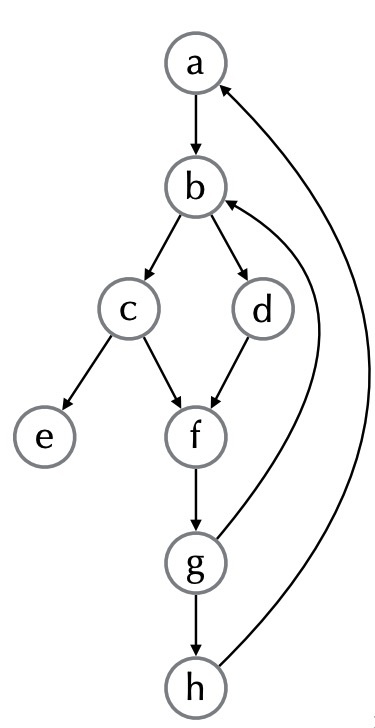
Example

In the above example, we have:

a dominates a,b,c,d,e,f,g,h
b dominates b,c,d,e,f,g,h
c dominates c,e
d dominates d
e dominates e
f dominates f,g,h
g dominates g,h
h dominates h
back-edges: g→b, h→a

Natural Loops

The natural loop of a back edge is the smallest set of nodes that includes the head and tail of the back edge, and has no predecessors outside the set, except for the predecessors of the header.

Single entry-point: header that dominates all nodes in the loop

Algorithm to Find Natural Loops:

Find the dominator relations in a flow graph
Identify the back edges
Find the natural loop associated with the back edge

Loop fusion & loop fission

Both loop fusion and loop fisson make good uses of the reference locality property. Loop fusion combines two loops into one while loop fission seperates one loop into two.

Loop fusion

  
// before fusion
int sum = 0;
for (int i = 0; i < n; ++i) {
  sum += a[i];
  a[i] = sum;
}
for (int i = 0; i < n; ++i) {
  b[i] += a[i];
}

// after fusion
int sum = 0;
for (int i = 0; i < n; ++i) {
  sum += a[i];
  a[i] = sum;
  b[i] += a[i];
}

Loop fission

  
// before fission
for (int i = 0; i < N; ++i) {
  a[i] = e1;
  b[i] = e2;
}


// after fission
for (int i = 0; i < N; ++i) {
  a[i] = e1;
}
for (int i = 0; i < N; ++i) {
  b[i] = e2;
}

Loop unrolling

Loop unrolling re-writes the loop body and each iteration of rewritten loop will perform several iterations of old loop.

  
// before unrolling
for (int i = 0; i < n; ++i) {
  a[i] = b[i] * 7 + c[i] / 13;
}

// after unrolling
for (int i = 0; i < n; i+=3) {
  a[i] = b[i] * 7 + c[i] / 13;
  a[i + 1] = b[i + 1] * 7 + c[i + 1] / 13;
  a[i + 2] = b[i + 2] * 7 + c[i + 2] / 13;
}

The benefit of loop unrolling is reducing branching penalty & end-of-loop-test costs.

Loop tiling

Loop tiling partitions a loop’s iteration space into smaller chunks or blocks, so as to help ensure data used in a loop stays in the cache until it is reused.

  
// before tiling
for (i = 0; i < n; i++) {
  c[i] = 0;
  for (j = 0; j < n; j++) {
    c[i] = c[i] + a[i][j] * b[j];
  }
}

// after tiling
for (i = 0; i < n; i += 4) {
  c[i] = 0;
  c[i + 1] = 0;
  for (j = 0; j < n; j += 4) {
    for (x = i; x < min(i + 4, n); x++) {
      for (y = j; y < min(j + 4, n); y++) {
        c[x] = c[x] + a[x][y] * b[y];
      }
    }
  }
}

Loop interchage

  
// before interchage
for (int j = 0; j < n; ++j) {
  for (int i = 0; i < n; ++i) {
    a[i][j] += 1;
  }
}

// after interchage
for (int i = 0; i < n; ++i) {
  for (int j = 0; j < n; ++j) {
    a[i][j] += 1;
  }
}

The benefit of loop interchange is reference locality.

Loop parallelization

Strength reduction

Computation Hoisting

Reference

Wiki: Control Flow Graph
Wiki: Loop Tiling
CSC D70: Compiler Optimization LICM (Loop Invariant Code Motion)